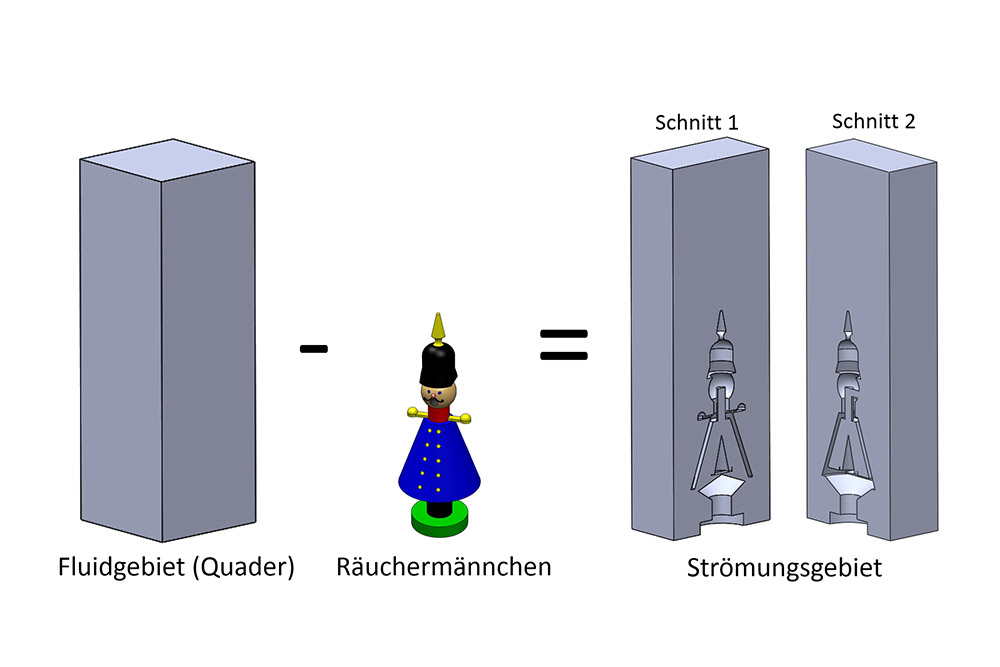
Im letzten Beitrag bildeten wir die Form des Räuchermannes im Computer nach und erstellten ein geometrisches Modell. Der Rauch strömt aber in den Hohlräumen, also genau dort, wo kein Holz ist. Wir müssen uns also nun um die Gebiete kümmern, die im Inneren des Räuchermanns und um ihn herum liegen. Dazu stellen wir uns einen Quader aus Luft vor, in dessen Mitte unser Räuchermann steht. Die Ränder dieses Quaders bilden die Grenzen unseres Modells. Darüber hinaus können wir nicht modellieren. Da wir die Gase (= Fluide) innerhalb dieses Quaders betrachten wollen, ist dies unser so genanntes Fluidgebiet. Fluide, also Gase, können überall in diesem Quader strömen. Eine Ausnahme nehmen genau die Stellen ein, an denen sich Holz befindet, also unser Räuchermann.

Im Modell heißt das: Wir müssen von unserem Fluidgebiet die Geometrie unseres Räuchermanns abziehen. Die Differenz aus dem kompletten Fluidgebiet und unserem Räuchermann ergibt dann das eigentliche Strömungsgebiet. Mathematisch bedeutet dies eine einfache Operation, denn unser Modell liegt ja schon im Rechner vor.

Wir ermittelten nun zumindest genau den Raum, in dem die Gase fließen können, die zum Räucherkerzchen führen und die den Rauch bilden. Aber wie kann man mathematisch das Strömen von Gasen beschreiben? In der theoretischen Betrachtung nutzt man dafür die Navier-Stokes-Gleichungen. Vereinfacht ausgedrückt stellen diese Gleichungen die Zusammenhänge zwischen Druck, Geschwindigkeit, Impuls und weiteren Parametern in einem strömenden Medium her. Das Problem ist, diese Gleichungen sind so komplex, dass sie sich nur in ausgewählten Spezialfällen lösen lassen. Man kann sie für den Computer vereinfachen, aber dann gelten diese Gleichungen nur für einen sehr kleinen Abschnitt des Raums.

Diese Vereinfachung führt uns aber zu einem Trick, den wir nutzen können, um das Problem doch noch zu lösen: Wir zerlegen einfach unser Strömungsgebiet in sehr viele kleine Elemente, in denen dann jeweils die Vereinfachung gilt. Je feiner aufgelöst diese Elemente sind, desto näher liegt unser Modell an der Realität. Das Berechnen der vereinfachten Gleichungen in sehr vielen kleinen Elementen kann ein Computer dann wieder sehr effizient übernehmen.

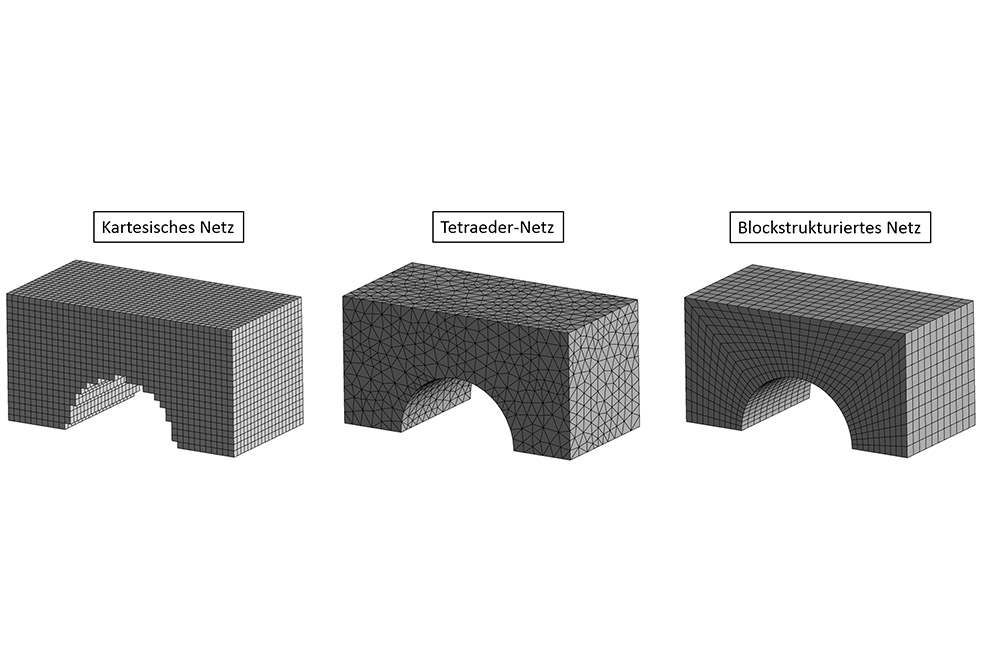
Aber wie zerlegen wir nun den Raum in gedachte Elemente, ohne dass Lücken bleiben? Die einfachste Variante ist sicher, kleine Quader zu benutzen. Dann erhält man ein Netz, das den realen Körper in quaderförmige Elemente teilt, so genannte Finite Volumen. Dieses Netz heißt kartesisches Netz. Eine nicht so offensichtliche Variante ist die Nutzung vieler kleiner Tetraeder. Auch mit Tetraedern kann man einen Raum lückenlos ausfüllen. In der Praxis gibt es noch weitere Möglichkeiten, beispielsweise blockstrukturierte Netze. Das Netz kann sogar an Stellen, an denen die Strömung besonders präzise untersucht werden soll, feiner aufgelöst werden als an anderen.

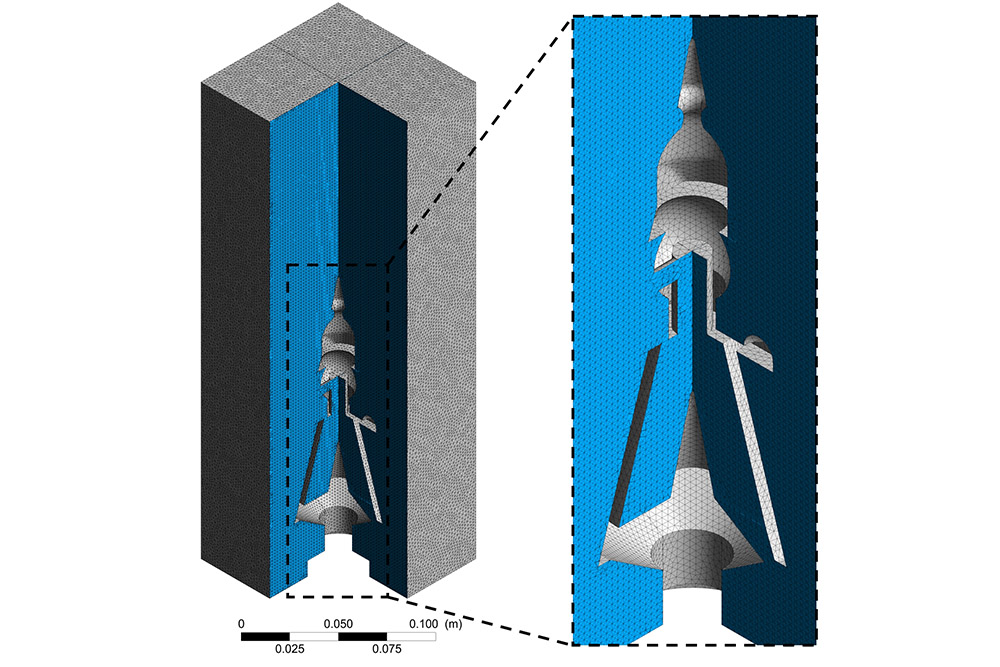
Nachdem wir nun unseren Gasraum präzise nachgebildet und vernetzt haben, bleibt ein letzter Schritt zu tun: Wir müssen das Modell parametrieren. Das heißt, mit physikalischen Parametern versehen. Jedem Netzelement, also jedem finiten Volumen, muss eine Stoffeigenschaft zugwiesen werden. So zum Beispiel welches Gas in dem Element enthalten sein soll (in unserem Fall Luft), welche Dichte und welche Viskosität das Gas hat, welche Temperatur und so weiter. Weiterhin müssen wir festlegen, an welchen Stellen Gas ein- und ausströmen (Inlet- und Outlet-Randbedingung) oder an welchen Wänden eine Strömungsgeschwindigkeit von Null herrschen soll (Haftbedingung). Haben wir dies alles bestimmt, können wir das Modell im Rechner starten. Für unseren Räuchermann wählten wir eine Tetraedervernetzung.

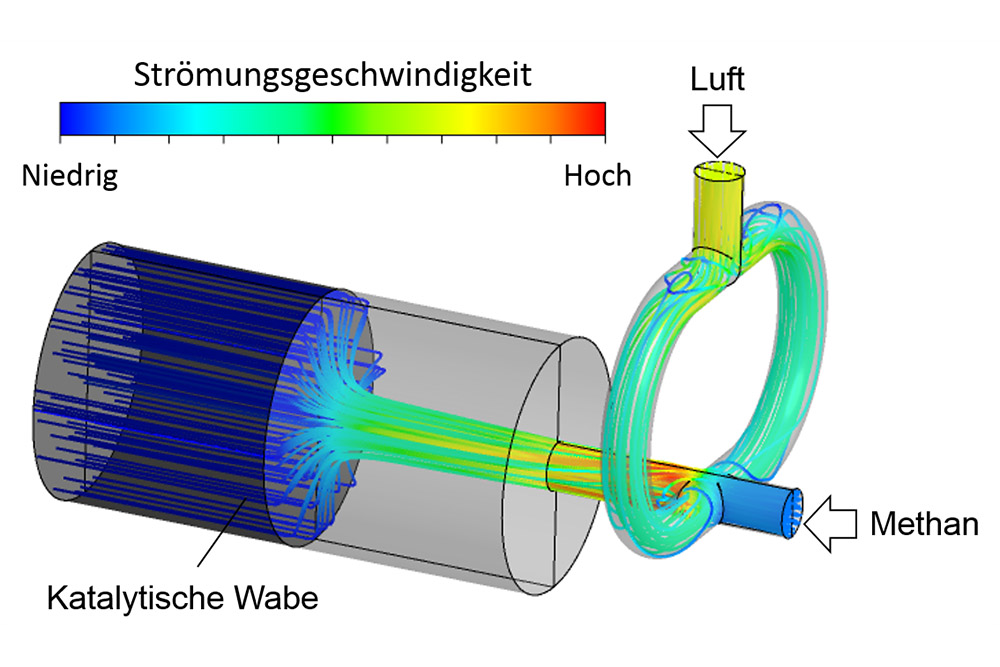
Die Computational Fluid Dynamics-Methode (CFD) ist ein extrem wichtiges Werkzeug für das Fraunhofer IKTS. Sehr viele Effekte in und an Maschinenbauteilen, in Reaktoren und in Energiesystemen – Gebiete auf denen das Fraunhofer IKTS arbeitet – haben mit strömenden Medien zu tun.

Wenn Sie mehr zur CFD und zum Modellieren und Simulieren wissen wollen, besuchen Sie unsere Themenseiten.

Hier entlang geht es zum vorherigen Beitrag: »Die Vermessung des Räuchermanns«. Hier gelangen Sie zum Nächsten: »Wie heiß wird die Räucherkerze?«.

Bleiben Sie darüber hinaus informiert: Melden Sie sich gern für unseren Newsletter an, lesen Sie in weitere Blogbeiträge rein oder folgen Sie uns auf LinkedIn, Instagram und YouTube. Wir freuen uns, mit Ihnen ins Gespräch zu kommen.